雅可比迭代求解Poisson方程.

Poisson方程是椭圆型偏微分方程的一个经典的模型方程，定义如下：

\[\begin{align} \nabla^2 u &= f , \; \text{in the inner} \\ \nabla^2 u &= g , \; \text{on the boundary} \end{align}\]

为了简单起见，我们考虑二维笛卡尔坐标系下，上式可写为：

\[\begin{equation} \left(\frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2}\right) u(x, y) = f(x,y) \end{equation}\]

为了数值求解该方程，我们可以将其离散到二维均匀网格上。设网格大小分别为 $\Delta x$ 和 $\Delta y$, 并使用 $u_{i,j}$ 表示坐标为 $(i, j)$ 处网格点的值。然后使用二阶中心差分格式代替上式的偏导数如下：

\[\begin{equation} \left(\frac{\partial^2 u}{\partial x^2}\right)_{i, j} = \frac{u_{i+1, j} - 2u_{i, j} + u_{i-1, j}}{(\Delta x)^2} \end{equation}\] \[\begin{equation} \left(\frac{\partial^2 u}{\partial y^2}\right)_{i, j} = \frac{u_{i, j+1} - 2u_{i, j} + u_{i, j-1}}{(\Delta y)^2} \end{equation}\]

简单起见假设 $\Delta x = \Delta y = 1$, 我们可以将Poisson方程重写如下：

\[\begin{equation} 4u_{i, j} - u_{i-1, j} - u_{i+1, j} - u_{i, j-1} - u_{i, j+1} = f_{i, j} \end{equation}\]

注意 $i, j$ 可以取计算域中的任意值，因而上面的方程实际上是一个大型的稀疏线性方程组，我们可以用经典的Jacobi迭代方法来求解(这并非求解该类问题的最优方法，但确实一种并行效率很好的迭代方法)。Jacobi迭代格式如下:

\[\begin{equation} u_{i,j}^{n+1} = \left(\frac{f_{i, j} + u_{i-1, j} + u_{i+1, j} + u_{i, j-1} + u_{i, j+1}}{4} \right)^n \end{equation}\]

这里的上标 $n$ 是迭代步数。

Poisson方程在一些情况下有简单的解析解，例如我们设域内 $f(x,y) = -4$， 边界处 $u(x, y) = x^2 + y^2 $ 时，其解析解为 $u(x,y) = x^2 + y^2$。或当域内 $f(x,y) = 4 \pi^2 \sin(2\pi x) \sin(2\pi y)$，边界处 $u(x, y) = 0$时，解析解为 $u(x,y) = \sin(2\pi x) \sin(2\pi y)$。

我们这里考虑Poisson方程的一种特殊形式，即当 $f=0$ 时的情况，此时我们将其称为Laplace方程。求解Laplace的Jacobi迭代方法与上述完全相同，且更容易理解：即没个网格点新一时间步的值是上一时间步四周网格点值的平均。

而当我们考虑热传导问题时 ($u = T$)，Laplace方程描述了在给定边界温度条件下，内部区域处于稳态时的温度分布。如果我们设上边界处温度为 1，其余边界温度为 0。那么稳态下温度分布如下：

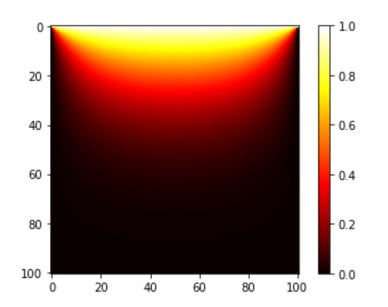
Jacobi迭代的串行程序

这个问题的求解非常简单，你可以直接参考串行代码: jacobi2d.f90.

我们使用两个二维数组 A 和 A_new 来分别储存不同时间步上网格的温度值。网格的排列如代码中注释所写：

! /*  data mesh arrangement
!  *  ny
!  *  ^
!  *  | (1,3)  
!  *  | (1,2)   
!  *  | (1,1)  (2,1)  (3,1)
!  *  ---------------------> nx
!  * 
!     for fortran language, data fill row first, (1,1),(2,1) ...
! */

网格坐标原点位于计算域左下角，向右为 $x$ 正方向，向上为 $y$ 正向。在Fortran语言中，这些网格点按行在内存空间中连续排列。

整个程序的计算过程相当简单，主演包含两大部分: jacobi 求解下一时间步的值 以及 swap 交换两个数组的值

subroutine jacobi(A, A_new, f, nx, ny)
    implicit none
    integer, intent(in) :: nx, ny
    real(8), intent(inout) :: A(0:nx+1, 0:ny+1), A_new(0:nx+1, 0:ny+1), f(0:nx+1, 0:ny+1)
    integer :: i, j

    do j = 1, ny
        do i = 1, nx
            A_new(i, j) = 0.25 * (A(i-1, j) + A(i+1, j) + A(i, j-1) + A(i, j+1) + f(i, j)) 
        enddo
    enddo

end subroutine jacobi

subroutine swap(A, A_new, nx, ny)
    implicit none
    integer, intent(in) :: nx, ny
    real(8), intent(inout) :: A(0:nx+1, 0:ny+1), A_new(0:nx+1, 0:ny+1)
    integer :: i, j

    do j = 1, ny
        do i = 1, nx
            A(i, j) = A_new(i, j)
        enddo
    enddo

end subroutine swap

而在主程序 main 里，我们就先initial初始化计算域，然后简单地重复这个过程直到迭代收敛或达到最大迭代步长。

do while(error_max > tolerance .AND. itc <= itc_max)
    itc =  itc + 1
    call jacobi(A, A_new, f, nx, ny)
    call swap(A, A_new)
    if(MOD(itc, 100) == 0) then
        error = check_diff(A, A_p, nx, ny)
        write(*, *) itc, error_max
    endif
enddo

检测收敛的方法很多，这里选择比较不同时间步 A 差的绝对值，并判断其最大值是否小于收敛条件。

雅可比迭代的MPI并行实现

在多核系统上加速上述代码的一种方法是使用MPI(Message Passing Interface)。使用MPI，我们可以将计算域分割为多个子计算域，每个处理器(核)负责一个子计算域的计算，MPI来处理计算域之间的信息同步。MPI并行的程序可以从这里获得： refer here to mpi codes

计算域的分割是MPI并行最重要的部分之一。对于这个均匀网格上的简答迭代问题，分割计算域需要考虑的问题也比较少。我们首先假设每个并行处理器的计算性能相同，那么只需要尽可能地平均分割计算域就可以实现负载均衡。考虑到在串行程序里，网格点是按行排列的，我们这里也优先考虑按行分割计算域如下图。然后将每个子计算域分配给处理器，这些处理器同时且独立地对自己所属的子计算域进行Jacobi迭代更新。但注意到，这些计算域的更新只有内点是全然局部的(只需要当前子计算域的值)，而上下边界的计算就需要用到相邻计算域的值。因此我们需要在上下边界处各布置一层虚拟节点(ghost points)。每个子计算域更新边界点前需要先从相邻计算域接受边界信息储存到虚拟节点上，并且将改边界节点的值发送给相邻计算域的虚拟节点。

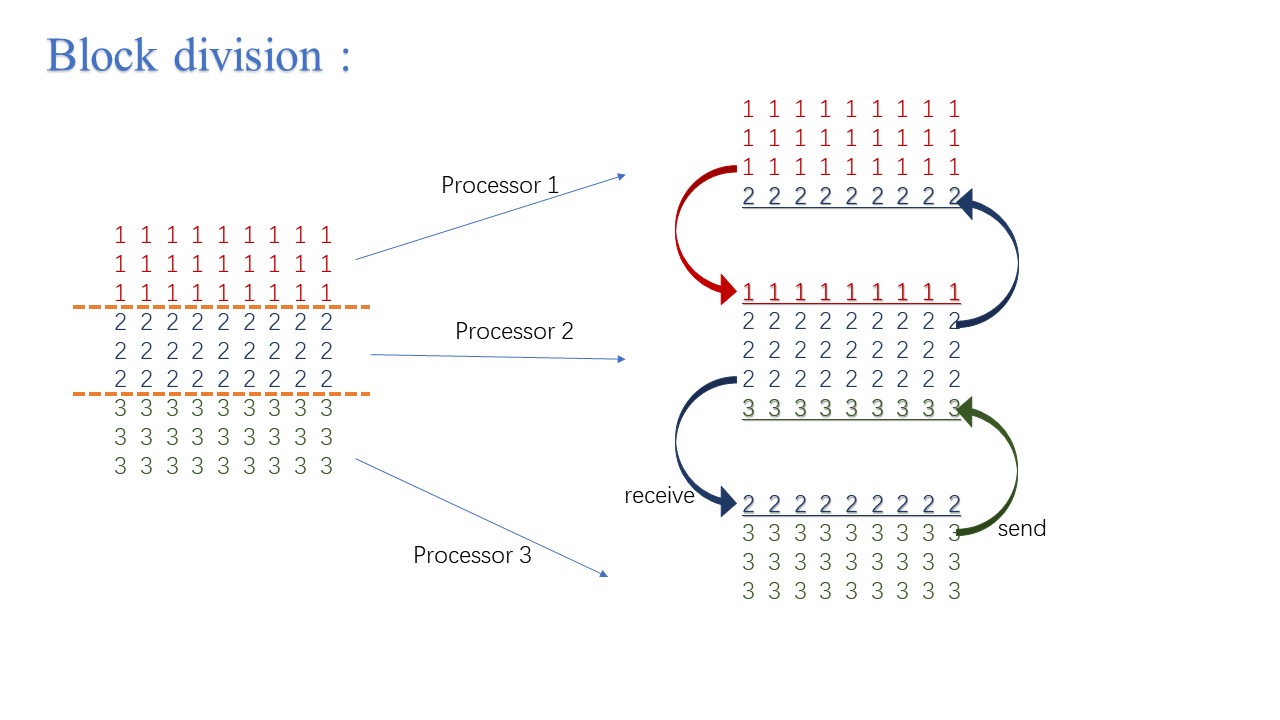
我们将这种分割方式称为1维切割，可以看到的是，随着所使用并行处理器数目的增加，每个处理器需要承担的计算负载持续减少，但其承担的信息传递任务一直保持不变，显然这并不是一种很好的实现方式，特别是对于大规模并行任务而言。一个更好的选择是使用如图所示的二维分割。

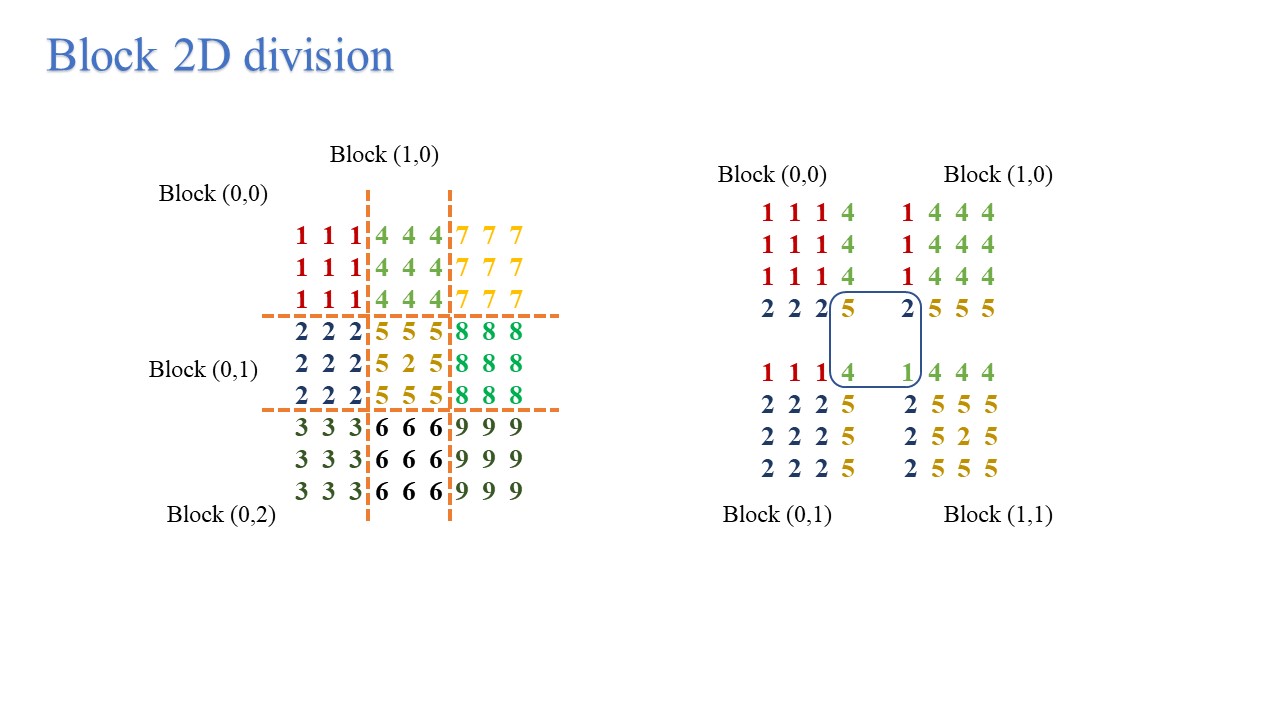
并行效率分析

尽管现有的实验条件不足，但我们可以对这个问题的计算时间和并行效率做一个简单的分析。简单起见我们假设 $nx = ny = n$。设传递一条边界的网格点消息所需的时间为 $T_{com} = s + rn$。$s$ 可看作消息传递时延或启动时间，所以当 $n$ 很大时， $T_{com} \approx rn$。

对于这个问题，当我们使用 $p$ 个处理器并行且使用1维分割时，消息传递所使用的时间总和为：

\[T_{c, 1d}(n, p) = 2 (s + rn)\]

而但我们使用二维分割时，假设两个维度的子块数目相同，则消息传递所使用的时间总和为：

\[T_{c, 2d} (n, p) = 4 \left(s + r \frac{n}{ \sqrt{p} } \right)\]

显然，只有当处理器个数大于等于 9 时，二维分割才可能使用更少的通信时间。

此外我们可以假设更新一个网格点信息所需的时间为 $f$, 那么串行程序的运行时间可记为：

\[T_s(n) = f * n^2\]

并行运行时间为：

\[T_{p, 1d} (n, p) = \frac{f n^2}{p} + T_{c}\]

我们定义并行程序的加速比为 $\text{speedup} = \frac{T_s}{T_p}$，并行效率分别为：$ \text{efficiency} = \frac{\text{speedup}}{p}$。对于一维分割而言：

\[\begin{equation*} \text{speedup}_{1d} = \frac{f n^2}{\frac{f n^2}{p} + 2(s + rn)} \end{equation*}\] \[\begin{aligned} \text{efficiency}_{1d} &= \frac{f n^2}{f n^2 + 2 p (s + rn)} \\ &= \frac{1}{1 + \frac{2p(s + rn)}{f n^2}} \end{aligned}\]

同样对于二维分割我们也可以得到：

\[\begin{equation*} \text{speedup}_{2d} = \frac{f n^2}{\frac{f n^2}{p} + 4 \left(s + r \frac{n}{ \sqrt{p} } \right)} \end{equation*}\] \[\begin{aligned} \text{efficiency}_{2d} = \frac{f n^2}{f n^2 + 4 p \left(s + r \frac{n}{ \sqrt{p} } \right)} \end{aligned}\]

通常而言，我们认为每个节点的计算耗时远远小于通信耗时，例如我们设 $f = 1$, $s = r = 10$。我们在下图给出了1维分割和二维分割并行效率的对比：

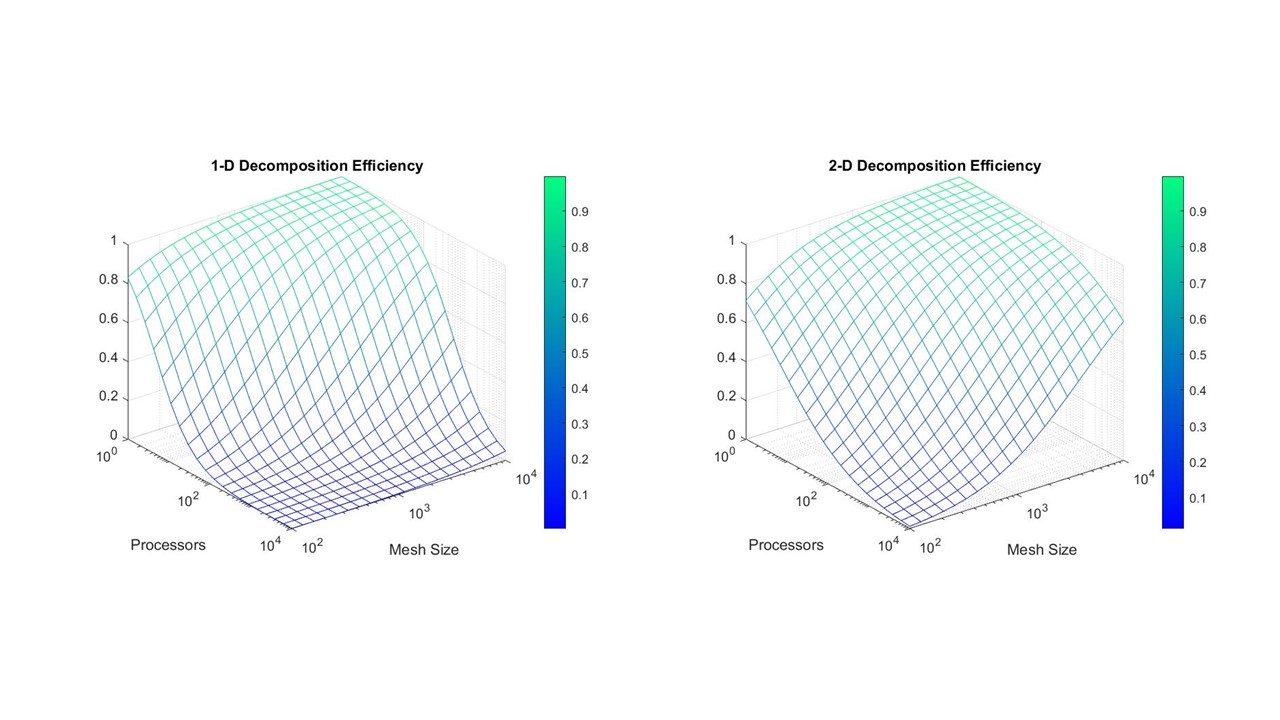
可以看到，在网格数目很多时，使用 1 维分割的并行效率很低，但此时二维分割仍旧有着很高的并行效率。

二维分割拓扑结构(start from scratch)

二维分割一大难点就是我们怎么设置分割后子计算域的拓扑结构。也就是说我们需要确定在使用 MPI_Comm_rank 后得到的处理器id(rank)对应的子区域是哪块，他的上下左右相邻子区域又是什么。

call MPI_Comm_rank(MPI_COMM_WORLD, rank, rc)

为了做到这些，我们可以给每个子区域一个块坐标(block index)，它表示这每个子区域在计算域中的位置。然后将处理器分配给这些子区域，分配方式任选，按行分配或按列分配都可以。这里我们以按行分配为例：

! /*  block arrangement
!  *  ny
!  *  ^
!  *  | (0,2)  
!  *  | (0,1)   
!  *  | (0,0)  (1,0)  (2,0)
!  *  ---------------------> nx
!  * 
!  *  rank assign : row first: rank0 = (0,0), rank1 = (1,0) ...
!  */

除了约定好子区域分配方式外，我们需要先确定每个维度的子块个数 nx_block 和 ny_block ，注意我们需要满足 nx_block * ny_block == num_processor 。之后我们就可以计算得到每个处理器分配得到的子区域的块坐标如下：

! block index
block_x = rank / ny_block
block_y = MOD(rank, ny_block)

每个子区域的相邻区域也可以由如下方式获得：

nbr_left = rank - 1
nbr_right = rank + 1
nbr_top = rank + nx_block
nbr_bottom = rank - nx_block

边界计算块的相邻子块需要进行特殊的处理，如果周期性边界条件，那么以最右侧子块为例，其相邻右侧子块就是同行的最左侧子块。但该问题不是周期性边界，最右侧子块没有右侧边界也无需与右侧交换任何信息，所以我们设其右边界为 MPI_PROC_NULL，这个值在MPI内部定义，以该值为目标的MPI_Send或MPI_Recv函数会自动忽略。

if (block_x == nx_block - 1) then
    nbr_right = MPI_PROC_NULL
endif

二维分割拓扑结构(better solution)

上述的做法虽然是正确的，但是却不一定是最高效的。特别是对于分布式系统而言，有些处理器之间的消息传递更为高效，有些却要花费更多时间，此时我们将这种决策交给编译器显然更为合理。而且这种笛卡尔坐标系下的计算域分块问题十分常见，因而MPI已经预定义了处理这种情况的方式。

首先我们使用已知可用的处理器总数 num_process来确定每个维度的子块个数 dims(2)， 然后用这个信息来创建一个新的通信器comm2d 。MPI_Cart_create 的第四个参数给出每个维度是否是周期条件，第五个参数就交给编译器决定是否重新排序处理器的 rank 来更高效利用硬件特性。

!!! Decomposition the domain
call MPI_Dims_create(num_process, 2, dims, rc)
call MPI_Cart_create(MPI_COMM_WORLD, 2, dims, periods, .true., comm2d, rc)

每个处理器在全局中的块坐标 coords 可以由如下函数得到：

call MPI_Cart_get(comm2d, 2, dims, periods, coords, rc)

要找到相邻子块的方法也很简单，可以使用 MPI_Cart_shift 函数。

! get the neighbors
call MPI_Cart_shift(comm2d, 0, 1, nbr_left, nbr_right, rc)
call MPI_Cart_shift(comm2d, 1, 1, nbr_bottom, nbr_top, rc)

网格无法均分问题

对于任意维度的分割问题，如果我们在该维度有100个网格点，但是只能分为 3 个子块，例如total_nx = 100, nx_block = 3，网格无法均分时怎样处理呢？答案很简单，我们可以设第一个子块 nx = 34， 其余两个子块 nx = 33 即可，这可以使用我们自定义的函数 decompose_1d 实现：

subroutine decompose_1d(total_n, local_n, rank, num_process)
    implicit none
    integer, intent(in) :: total_n, rank, num_process
    integer, intent(out) :: local_n

    local_n = total_n / num_process
    if (rank < MOD(total_n, num_process)) then
        local_n = local_n + 1
    endif
end subroutine decompose_1d

对于多维问题只需要在各个维度调用该函数即可：

call decompose_1d(total_nx, nx, coords(1), dims(1))
call decompose_1d(total_ny, ny, coords(2), dims(2))

不连续的信息交换

在二维分割的情况下，每个子计算域的四个边界都各有一层虚拟网格点，按照 Fortran 语言的内存特性，我们在发送接受信息时，上下边界在内存上是连续的，因而以点对点通信的发送操作为例，我们可以直接发送上边界的信息如下：

call MPI_Send(A(1,ny), nx, MPI_DOUBLE_PRECISION, nbr_top, 0, MPI_COMM_WORLD, rc)

MPI_Send 的前三个参数分别代表待发送消息的内存起始地址，数据个数和数据类型。在处理左右边界时，边界网格点在内存中位置不连续，此时我们可以在每个网格点调用一次 MPI_Send ，但是这种方式的开销太大(感兴趣的读者可以自行尝试)。一种可选的方式是建立一个连续的缓存区存储将要发送或接受的消息。

do j = 1, ny
    send_buf(j) = A(1, j)
enddo
call MPI_Send(send_buf, ny, MPI_DOUBLE_PRECISION, nbr_left, 0, comm2d, rc)

call MPI_Recv(recv_buf, ny, MPI_DOUBLE_PRECISION, nbr_left, 1, comm2d, MPI_STATUS_IGNORE, rc)
do j = 1, ny
    recv_buf(j) = A(0, j)
enddo

但我们注意到这种方式在消息发送或接受时均需要额外复制移动一次消息，怎样避免这样的开销呢？MPI 灵活的数据类型定义给出了很巧妙的解决方式。既然要发送的消息在内存中不连续，那么我们可以直接告诉MPI接下来那你要发送的消息就是在内存中不连续存储的，但是它在内存中的分布服从某种规律，你可以按这种规律去读取并发送数据。这种特殊的存储规律就是我们新定义的数据类型 MPI_Data_type。上面使用的 MPI_DOUBLE_PRECISION 就是一种固定长度连续内存的MPI内置数据类型。而为了处理左右边界信息，我们可以定义一种边界数据类型 column_y 如下:

! construct the datatype for the exchange in y direction(non-contiguous)
call MPI_Type_vector(ny+2, 1, nx+2, MPI_DOUBLE_PRECISION, column_y, rc)     ! two ghost layers
call MPI_Type_commit(column_y, rc)

这个数据类型就代表了整个一列边界的内存排列方式，因而左边界的发送函数可写为：

call MPI_Send(A(1,1), 1, column_y, nbr_left, 0, comm2d, rc)

信息交换调度

尽管这个问题的信息交换很简单，但如果不注意信息传递的先后顺序以及发送与接受的配合，那仍旧很容易写出并行效率很低甚至导致死锁的程序。

Locked

首先我们考虑一种实现方式，每个计算域先接受下侧发来的信息，然后向下侧发送信息，再向上侧发送信息，然后接受上侧传来的信息，代码如下。左右两侧的信息传递方式类似。

call MPI_Recv(A(1,0), nx, MPI_DOUBLE_PRECISION, nbr_bottom, 1, comm2d, MPI_STATUS_IGNORE, rc)
call MPI_Send(A(1,1), nx, MPI_DOUBLE_PRECISION, nbr_bottom, 0, comm2d, rc)

call MPI_Send(A(1, ny), nx, MPI_DOUBLE_PRECISION, nbr_top, 1, comm2d, rc)
call MPI_Recv(A(1, ny+1), nx, MPI_DOUBLE_PRECISION, nbr_top, 0, comm2d, MPI_STATUS_IGNORE, rc) 

这就是一种典型的容易导致死锁的实现方式。虽然再改问题里由于周期性边界条件的存在不会真正导致死锁，但是并行效率会大幅下降。简单分析可知，每个区块最开始都先执行 MPI_Recv 但是此时却没有区块执行对应的 MPI_Send。如果我们将上述代码的前两行调换位置，即先执行 MPI_Send，此时代码的效率就严重依赖于问题规模的大小和MPI系统缓存区的大小。因为此时，MPI会尽量缓存消息后返回，然后等到对应的接收函数启动时才真正发送。当缓存区不够时，就会出现上面提到的死锁问题。

Ordered

为了解决上述问题，我们可以自行调度消息传递顺序。例如在传递从下到上的消息时，我们可以指定偶数坐标的区块先发送消息，此时对应的奇数坐标的区块接受消息。这样一来，所有的发送操作都有其对应的接受操作几乎同时进行，可以提高并行的效率。

! exchange messages along y (ghost row)
! even index
if (MOD(coords(2), 2) == 0) then
    ! message passing to top(j++)
    call MPI_Send(A(1, ny), nx, MPI_DOUBLE_PRECISION, nbr_top, 1, comm2d, rc)
    call MPI_Recv(A(1, 0), nx, MPI_DOUBLE_PRECISION, nbr_bottom, 1, comm2d, MPI_STATUS_IGNORE, rc)

    ! message passing to bottom(j--)
    call MPI_Send(A(1, 1), nx, MPI_DOUBLE_PRECISION, nbr_bottom, 0, comm2d, rc)
    call MPI_Recv(A(1, ny+1), nx, MPI_DOUBLE_PRECISION, nbr_top, 0, comm2d, MPI_STATUS_IGNORE, rc)
! odd index
else
    ! message passing to top(j++)
    call MPI_Recv(A(1, 0), nx, MPI_DOUBLE_PRECISION, nbr_bottom, 1, comm2d, MPI_STATUS_IGNORE, rc)
    call MPI_Send(A(1, ny), nx, MPI_DOUBLE_PRECISION, nbr_top, 1, comm2d, rc)

    ! message passing to bottom(j--)
    call MPI_Recv(A(1, ny+1), nx, MPI_DOUBLE_PRECISION, nbr_top, 0, comm2d, MPI_STATUS_IGNORE, rc)
    call MPI_Send(A(1, 1), nx, MPI_DOUBLE_PRECISION, nbr_bottom, 0, comm2d, rc)
endif

Sendrecv

这是一种我们推荐使用且十分适用于该情况的处理方式，即适用 MPI_Sendrecv 函数。它只是指定我们需要进行发送和接受两个操作，编程简单，但每个区块这两个操作的先后顺序则交给MPI系统自行调度，因而效率也很高。

subroutine exchange_message(A, nx, ny, coords, comm2d, column_y, nbr_left, nbr_right, nbr_bottom, nbr_top)
    use mpi
    implicit none
    integer, intent(in) :: nx, ny, comm2d, column_y, coords
    integer, intent(in) :: nbr_left, nbr_right, nbr_top, nbr_bottom
    real(8), intent(in) :: A(0:nx+1, 0:ny+1)
    integer :: i, j, rc

    ! corners don't matter in this problem

    ! exchange messages along y (ghost row)
    ! message passing to top(j++)
    call MPI_Sendrecv(A(1, ny), nx, MPI_DOUBLE_PRECISION, nbr_top, 0, &
                    A(1, 0), nx, MPI_DOUBLE_PRECISION, nbr_bottom, 0, &
                    comm2d, MPI_STATUS_IGNORE, rc)
    ! message passing to bottom(j--)
    call MPI_Sendrecv(A(1, 1), nx, MPI_DOUBLE_PRECISION, nbr_bottom, 1, &
                    A(1, ny+1), nx, MPI_DOUBLE_PRECISION, nbr_top, 1, &
                    comm2d, MPI_STATUS_IGNORE, rc)

    ! exchange messages along x (ghost column)
    ! message passing to right(i++)
    call MPI_Sendrecv(A(nx, 1), 1, column_y, nbr_right, 0, &
                    A(0, 1), 1, column_y, nbr_left, 0, &
                    comm2d, MPI_STATUS_IGNORE, rc)
    ! message passing to left(i--)
    call MPI_Sendrecv(A(1, 1), 1, column_y, nbr_left, 1, &
                    A(nx+1, 1), 1, column_y, nbr_right, 1, &
                    comm2d, MPI_STATUS_IGNORE, rc)
end subroutine exchange_message

Non-block

我们可以使用非阻塞式通信代替阻塞式通信，与阻塞式通信需要满足一定条件才能返回不同，非阻塞式通信可以立即返回，而通信真正开始的时间则交给MPI系统。但我们需要在最后显示地测试或等待通信完成。

! exchange messages along y (ghost row)
! message passing to top(j++)
call MPI_Irecv(A(1, 0), nx, MPI_DOUBLE_PRECISION, nbr_bottom, 1, comm2d, req(1), rc)
call MPI_Isend(A(1, ny), nx, MPI_DOUBLE_PRECISION, nbr_top, 1, comm2d, req(2), rc)

! message passing to bottom(j--)
call MPI_Irecv(A(1, ny+1), nx, MPI_DOUBLE_PRECISION, nbr_top, 0, comm2d, req(3), rc)
call MPI_Isend(A(1, 1), nx, MPI_DOUBLE_PRECISION, nbr_bottom, 0, comm2d, req(4), rc)

! exchange messages along x (ghost column)
! message passing to right(i++)
call MPI_Irecv(A(0, 1), 1, column_y, nbr_left, 0, comm2d, req(5), rc)
call MPI_Isend(A(nx, 1), 1, column_y, nbr_right, 0, comm2d, req(6), rc)

! message passing to left(i--)
call MPI_Irecv(A(nx+1, 1), 1, column_y, nbr_right, 1, comm2d, req(7), rc)
call MPI_Isend(A(1, 1), 1, column_y, nbr_left, 1, comm2d, req(8), rc)

call MPI_Waitall(8, req, MPI_STATUSES_IGNORE, rc)

使用非阻塞式通信重叠通延时信和计算

非阻塞式通信最大的作用除了避免死锁外，就是能掩盖通信延时。在很多情况下，通信延时是MPI并行效率的最大死敌。但如果我们可以把通信与计算重叠，做到在通信时同时进行计算工作，就像用洗衣机洗衣服的时候同时做饭，那样并行效率就可以有很大提升。但是我们需要注意的是，有些情况下，MPI并行的通信延时很小，重叠通信和计算带来的改善也很小，而更重要的是，有些情况下，并行硬件可能不支持通信和计算同时进行，那么此时如果你发现自己的程序性能没有提高，很可能不是你的错。

重叠通信和计算是通过非阻塞式通信完成的，在非阻塞式通信完成前，它的缓存区都是不安全的，也就是说我们不能在这个阶段使用它。因而对于这个Jacobi迭代问题，我们可以先启动通信交换边界点信息，。

call MPI_Irecv(A(1, 0), nx, MPI_DOUBLE_PRECISION, nbr_bottom, 1, comm2d, req(1), rc)
! ... 
call MPI_Isend(A(1, 1), 1, column_y, nbr_left, 1, comm2d, req(8), rc)

然后在通信过程中计算更新内点：

do j = 2, ny-1
    do i = 2, nx-1
        A_new(i, j) = 0.25 * (A(i-1, j) + A(i+1, j) + A(i, j-1) + A(i, j+1) + f(i, j)) 
    enddo
enddo

最后在确定通信完成后再计算边界点的值。

! wait messages
call MPI_Waitall(8, req, MPI_STATUSES_IGNORE, rc)

!calculate the boundary
do j = 1, ny, ny-1
    do i = 1, nx
        A_new(i, j) = 0.25 * (A(i-1, j) + A(i+1, j) + A(i, j-1) + A(i, j+1) + f(i, j)) 
    enddo
enddo
do i = 1, nx, nx-1
    do j = 1, ny
        A_new(i, j) = 0.25 * (A(i-1, j) + A(i+1, j) + A(i, j-1) + A(i, j+1) + f(i, j)) 
    enddo
enddo

并行结果

我们设 total_nx = total_ny = 2000， 运行 1000 个时间步长，记录其所花时间。运行的机器和环境参数如下：

	参数
Linux发行版	CentOS Linux release 7.9.2009 (Core)
处理器	Intel(R) Xeon(R) Platinum 8160 CPU @ 2.10GHz
编译器	ifort (IFORT) 19.0.0.117 20180804
CPU核心数/线程数	24核48线程

串行程序的运行时间为 9.485 s。不同处理器下采用不同消息传递调度方式的结果如下，第一列代表在每个维度下的处理器个数。

	Locked	Ordered	Sendrecv	non-blocked	overlap
2x1	4.873	4.893	4.961	4.921	4.833
5x1	2.664	2.751	2.618	2.603	2.762
9x1	2.386	2.261	2.246	2.261	2.321
1x9	2.086	2.013	2.081	2.044	2.113
3x3	2.151	2.132	2.152	2.167	2.233

结果与预期有所差别，我们发现预计的死锁现象并没有发生，这个原因可能是编译器的优化，或者MPI系统提供了足够的缓存区。而这个问题需要传递的数据量较小，缓存消息带来的开销影响也不大。但我们还是必须注意，这种程序正确性和效率依赖MPI系统的实现方式是不可取的。其他几种实现方式的效率差别不大，特别是我们发现即使实现了计算和通信重叠，但并行效率反而有所下降，这可能是因为该系统硬件不支持计算的同时通信，因而我们无法重叠两者，反而在更新边界点时无法有效利用缓存，增加了额外的开销。此外多维分割的优点在处理器数目较小时也体现不明显。

并行算法改进

讨论并行效率，加速比等问题当然很有必要，但这些并不是衡量一个并行算法实现好坏的所有重要指标。因为这仅仅是相对与特定的串行实现而言的，那么这种串行实现，或者说算法而言，一定是最优的吗？对于这个问题而言答案是否定的。

程序结构优化

回头研究上面给出的串行程序，我们会发现我们其实让数组A 和 A_new 分别交替存储新旧时间步的值。这样一来我们就不再需要 swap 函数，减少了数据在内存中的移动次数。新的迭代方式如下：

do while(error_max > tolerance .AND. itc <= itc_max)
    itc =  itc + 2
    call jacobi(A, A_new, f, nx, ny)
    call jacobi(A_new, A, f, nx, ny)
    if(MOD(itc, 100) == 0) then
        error = check_diff(A, A_p, nx, ny)
        write(*, *) itc, error_max
    endif
enddo

优化后结果如下：

串行时间：6.331 s

	Locked	Ordered	Sendrecv	non-blocked	overlap
2x1	3.128	3.140	3.100	3.100	3.141
5x1	1.803	1.740	1.753	1.755	1.784
9x1	1.611	1.470	1.460	1.461	1.494
1x9	1.427	1.437	1.426	1.430	1.464
3x3	1.416	1.420	1.390	1.386	1.451

可以看到使用相同处理器数目下运行时间较优化前均减少了约 1/3 。而且去掉 swap 函数后，二维分割的效果也初步显现了。而且我们相信，随着处理器数目的继续增加，二维分割带来的优势必将逐渐增大。

迭代算法改进

前面提到其实 Jacobi 迭代不是求解 Poisson 问题的最佳迭代方式，只是它的并行效率比较高。而比较而言，Gauss–Seidel 迭代是一种收敛速度更快的迭代方式，但是它的并行效率却很差。因而一个非常流行的算法是红黑高斯-赛德尔迭代法或称为red-black ordering。他有着很高的并行效率且收敛速度远快于Jacobi迭代。